Question

A 100-turn coil with an average radius of 0.04 m is placed in a uniform magnetic field so that ϕ = 60°. The strength of the field increases at a rate of 0.250 T/s. What is the magnitude of the resulting emf?

Answer 1

`\epsilon=0.063 V`

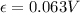
Step-by-step explanation:

Accord to Faraday's law, the magnitude of the electromotive force is given by:

`\epsilon=(d\Phi_B)/(dt)(1)`

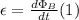
Magnetic flux is defined as:

`\Phi_B=NBAcos(\phi)`

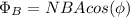
Here, N are the coil turns, B is the magnitud of the magnetic field, A is the area and
`\phi` is the angle between the magnetic field lines and the normal to A.

Then:

`(d\Phi_B)/(dt)=N(dB)/(dt)Acos(\phi)(2)`

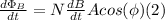
Replacing (2) in (1) we have:

`\epsilon=N(dB)/(dt)Acos(\phi)\\\epsilon=100*0.25(T)/(s)*pi*(0.04m)^2cos(60^\circ )\\\epsilon=0.063 V`

Answer 2

Five

This is exactly like your question 2. You need only substitute the given numbers here.

Givens

• N = 100 turns
• delta B = 0.25
• r = 0.04
• Area = pi * r^2 = 3.14 * 0.04^2 = 5.02 * 10^-3
• Cos 60 = 1/2 = 0.5

Formula

e = N * delta B * Area * cos phi

Solution

e = - 100 * 0.25 * 5.02 * 10^-3 * 0.5

e = 0.0628 = 0.063

Answer

A

Six

This is a notes question. The result is a sine curve. I don't know how they are counting the change in direction. Is a rising curve different from a falling curve? For sure going from plus to minus is a change in direction, but I still don't know how to count it. It will depend on what you have been told.

I would answer 4 but this is by no means certain. The only other possible answer is 2