Question

Which of the following is a solution of z^5 = 1 + √3 i?

5√2 (cos150° + isin150°)
5√2 (cos156° + isin156°)
5√2 (cos174° + isin174°)
5√2 (cos204° + isin204°)

Please show me how to work it out.

Answer 1

Option 2 is right

Explanation:

Given that

`z^5=1+√(3) i`

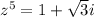
We can write this in polar form with modulus and radius

`|z^5|= √(1+3) =2\\tan of Angle t =√(3) \\`

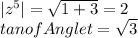
Hence angle = 60 degrees and

`|z^5|= 2(cos60+isin60)`

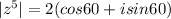
Since we have got 5 roots for z, we can write 60, 420, 780, etc. with periods of 360

Using Demoivre theorem we get 5th root would be

5th root of 2 multiplied by 1/5 th of 60, 420, 780,....

`z= \sqrt[5]{2} (cos12+isin12)\\z=\sqrt[5]{2} (cos84+isin84)\\\\z=\sqrt[5]{2} (cos156+isin156)\\\\z=\sqrt[5]{2} (cos228+isin228)\\\\z=\sqrt[5]{2} (cos300+isin300)\\`

Out of these only 2nd option suits our answer

Hence answer is Option 2.