Question

Determine any data values that are missing from the table, assuming that the data represent a linear function.

a. Missing x:13 Missing y:20
b. Missing x:13 Missing y:19
c. Missing x:11 Missing y:20
d. Missing x:11 Missing y:19​

Answer 1

• d. Missing x:11 Missing y:19​

Explanation:

It can be determined that the function is:

• y = 0.5x + 12.5

So missing x is:

• 18 = 0.5x + 12.5 ⇒ 0.5x = 5.5 ⇒ x = 11

Missing y is:

• y = 13*0.5 + 12.5 = 19

Missing numbers are:

• x= 11 and y = 19

Correct choice is d.

Answer 2

FIRST METHOD

Answer:

• Missing x = 11

• Missing y = 19

Explanation:

Given the table

x y

7 16

9 17

Missing x 18

13 Missing y

From the table, it is clear that y-values are incremented by 1 unit and the x-values are incremented by 2 units.

i.e.

y = 17-16 = 1

y = 18-17 = 1

as 19-18 = 1

Thus,

Thus, the value of Missing y = 19

also the x-values increment by 2.

i.e.

x = 9-7 = 2

as x = 11 - 9 = 2

Thus, Missing x = 11

Therefore,

• Missing x = 11

• Missing y = 19

2ND METHOD

Given that the table represents a linear function, so the function is a straight line.

Taking two points

• (7, 16)

• (9, 17)

Finding the slope between (7, 16) and (9, 17)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(7,\:16\right),\:\left(x_2,\:y_2\right)=\left(9,\:17\right)`

`m=(17-16)/(9-7)`

`m=(1)/(2)`

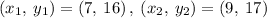
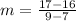
Using the point-slope form to determine the linear equation

`y-y_1=m\left(x-x_1\right)`

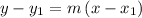
where m is the slope of the line and (x₁, y₁) is the point

substituting the values m = 1/2 and the point (7, 16)

`y-y_1=m\left(x-x_1\right)`

`y-16=(1)/(2)\left(x-7\right)`

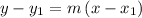
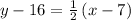
Add 16 to both sides

`y-16+16=(1)/(2)\left(x-7\right)+16`

`y=(1)/(2)x+(25)/(2)`

Thus, the equation of the linear equation is:

`y=(1)/(2)x+(25)/(2)`

Now substituting y = 18 in the equation

`18=(1)/(2)x+(25)/(2)`

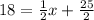
Switch sides

`(1)/(2)x+(25)/(2)=18`

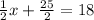
subtract 25/2 from both sides

`(1)/(2)x+(25)/(2)-(25)/(2)=18-(25)/(2)`

`(1)/(2)x=(11)/(2)`

`x=11`

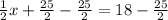
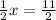
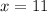
Thus, the value of missing x = 11 when y = 18

Now substituting x = 13 in the equation

`y=(1)/(2)\left(13\right)+(25)/(2)`

`y=(13)/(2)+(25)/(2)`

`y=(13+25)/(2)`

`y=(38)/(2)`

`y = 19`

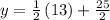
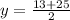
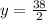
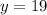
Thus, the value of missing y = 19 when x = 13

Hence, we conclude that:

• The value of missing x = 11

• The value of missing y = 19

Hence, option D is true.