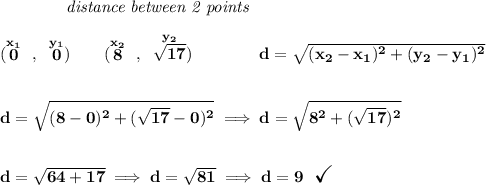Question

A circle centered at the origin contains the point (0,-9). Does (8, sqr 17) also lie on the circle?

Answer 1

Check the picture below.

since the circle is centered at the (0,0) origin, and a point on it is at (0, -9), its radius is simple the distance between those two, or r = 9.

if the second point is also on the circle, it must also be 9 units away from the origin.

`\bf ~~~~~~~~~~~~\textit{distance between 2 points} \\\\ (\stackrel{x_1}{0}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{√(17)})\qquad \qquad d = √(( x_2- x_1)^2 + ( y_2- y_1)^2) \\\\\\ d=\sqrt{(8-0)^2+(√(17)-0)^2}\implies d=\sqrt{8^2+(√(17))^2} \\\\\\ d=√(64+17)\implies d=√(81)\implies d=9~~\textit{\Large \checkmark}`