Question

In 1994, Susan Williams of California blew a bubble-gum bubble with a diameter of 58.4 cm. If this bubble were rigid and the centripetal acceleration of the equilateral points of the bubble were 8.5*10^-2 m/s^2, what would the tangential speed of those points be?

Answer 1

0.158 m/s

Step-by-step explanation:

The centripetal acceleration of the equilateral points of the bubble is given by

`a=(v^2)/(r)`

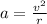
where

v is the tangential speed

r is the radius of the bubble

In this problem, we have:

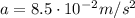`a=8.5\cdot 10^(-2) m/s^2` is the centripetal acceleration

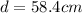`d=58.4 cm` is the diameter of the bubble, so the radius is

`r=(58.4 cm)/(2)=29.2 cm=0.292 m`

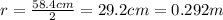
Therefore, we can re-arrange the previous equation to find the tangential speed of the equilateral points:

`v=√(ar)=\sqrt{(8.5\cdot 10^(-2) m/s^2)(0.292 m)}=0.158 m/s`