Question

Write an equation for the line that passes through (4,-6) and (-7,-6). Is the line parallel or perpendicular to the y-axis?

Answer 1

y = -6, perpendicular

Explanation:

You can use the points to find the slope of the line:

`m=(y_(2)-y_(1))/(x_(2)-x_(1)) =(-6-(-6))/(-7-4) =(-6+6)/(-7-4)=(0)/(-11)=0`

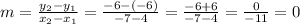
Then, using point-slope form, choose one set of coordinates to use for y1 and x1:

`y-y_(1)=m(x-x_(1))`

`y-(-6)=0(x-4)`

`y+6=0`

`y=-6`

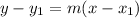
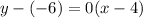
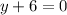
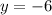
Since the slope of the line is zero, it's a horizontal line. The y-axis is a vertical line, which means that the line is perpendicular to the y-axis.