Explanation:
It is given that,
Initial velocity of the ball, u = 64 ft/s
The distance of the ball from the ground is given by the following relation as :
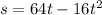
t is the time taken
(a) Let t is the time when the ball strike the ground. When it strikes the ground, s = 0
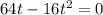
On solving the above quadratic equation, we get the value of t as t = 4 seconds. So, at 4 seconds the ball will strike the ground.
(b) Let t is the time when the ball is more than 28 feet above the ground. So,
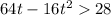
On solving the above inequalities, we get the value of t as :
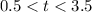
So, from 0.5 seconds to 3.5 seconds, the ball is at the height of 28 feet above the ground.
Hence, this is the required solution.