Answer:
Part 5)
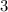
Part 6)
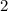
Par 7)
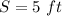
Part 8)
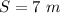
Explanation:
Part 5) we have
![\sqrt[3]{27}](https://img.qammunity.org/2020/formulas/mathematics/high-school/2vajawwf8jn7vk72b8sbgveo1dmsmnvdxx.png)
we know that
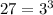
substitute
![\sqrt[3]{27}=\sqrt[3]{3^(3)}=3^{(3)/(3)}=3](https://img.qammunity.org/2020/formulas/mathematics/high-school/e202sct2wfmtrcxkja2edbljq9mvge0txd.png)
Part 6) we have
![\sqrt[4]{16}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/apfutj1ac4hnjurcpvdrvbck09xvq77xxb.png)
we know that
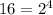
substitute
![\sqrt[4]{16}=\sqrt[4]{2^(4)}=2^{(4)/(4)}=2](https://img.qammunity.org/2020/formulas/mathematics/high-school/iarig4pjypi6n1ycttpuhzzp8wawyan55q.png)
Part 7) we know that
The volume of the cube is equal to
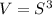
where
S is the length side of the cube
In this problem we have
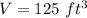
substitute
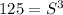
![S=\sqrt[3]{125}=\sqrt[3]{5^(3)}=5^{(3)/(3)}=5\ ft](https://img.qammunity.org/2020/formulas/mathematics/high-school/gajzq3qqipnb53s2pg96055vmks9jlhmc2.png)
Part 8) we know that
The volume of the cube is equal to
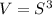
where
S is the length side of the cube
In this problem we have
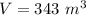
substitute
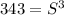
![S=\sqrt[3]{343}=\sqrt[3]{7^(3)}=7^{(3)/(3)}=7\ m](https://img.qammunity.org/2020/formulas/mathematics/high-school/bbixk9a0lxowx0sb6uymdeghm0buv6c6jt.png)