Answer:
Figure 4 ⇒ x =
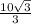 = 5.774
= 5.774
y =
 = 2.887
= 2.887
Figure 5 ⇒ x = 7
y =
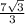 = 4.041
= 4.041
Explanation:
Figure 4:
∵ The Δ is right triangle
∴ Use trigonometry function
∵ 5/x = sin(60°)
∴ x = 5/sin(60°) =
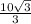 = 5.774
= 5.774
∵ 5/y = tan(60°)
∴ y = 5/tan(60°) =
 = 2.887
= 2.887
Figure 5:
∵ The Δ is right triangle
∴ Use trigonometry function
∵
 = sin(60°)
= sin(60°)
∴ x =
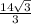 ×sin(60°) = 7
×sin(60°) = 7
∵
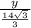 = cox(60°)
= cox(60°)
∴ y =
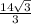 ×cos(60°)=
×cos(60°)=
 = 4.041
= 4.041