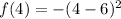Question

Match the function with the graph.

Answer 1

Option a.

Explanation:

It should be noted in the attached graph that the vertex of the function is in point (6.0). and it is reflected in the y axis.

Therefore you should look for a quadratic function of the form
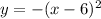`y = -(x-6)^2` The option that matches is option a.

You can test this answer by replacing values in the function and seeing that it matches the graph.

For example, observe in the graph that the point (4, -4) belongs to the function. Then when replacing f(4) in the function
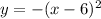`y = -(x-6)^2` you must obtain f(4) = -4

`f(4) = -(4-6)^2`

`f(4) = -4`

Answer 2

ANSWER

`g(x) = - {(x - 6)}^(2)`

EXPLANATION

The graph has a maximum turning point (vertex) with coordinates (6,0).

The vertex form of the parabola is


`g(x) = a {(x - h)}^(2) + k`

Where

`a = - 1`


`h = 6`


`k = 0`

We substitute the values into the formula to obtain the function equation.

The required function is


`g(x) = - 1 {(x - 6)}^(2) + 0`
We simplify to get,


`g(x) = - {(x - 6)}^(2)`

The correct answer is A.