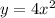Question

which equation is the quadratic variation equation for the relatonship? the variable y varies directly with x^2 and y=36 when x=3

Answer 1

For this case we have a direct variation of the form:

`y = kx ^ 2`

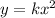
Where,

• k: proportionality constant

We must find the value of k.

For this, we use the following data:

`y = 36\\x = 3`

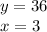
Therefore, replacing values we have:

`36 = k (3) ^ 2`

Rewriting:

`36 = 9k`

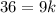
Clearing the value of k we have:

`k = \frac {36} {9}\\k = 4`

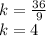
Therefore, the direct variation equation is given by:

`y = 4x ^ 2`

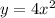
Answer:

The quadratic variation equation for the relatonship is:

`y = 4x ^ 2`