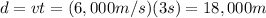Question

Equations to use: v= λ ∙ f v=d/t

b. A guitar string has a length of 0.90 m. When you pluck it, it plays a “C” that has a frequency of 256 Hz. How fast is the wave moving back and forth along the string? (

c. In a train track made of solid steel, sound waves travel extremely fast – about 6,000 m/s. If a train’s vibration travels for 3 seconds, how far will it move?

Answer 1

b. 460.8 m/s

Step-by-step explanation:

The relationship between the speed of the wave along the string, the length of the string and the frequency of the note is

`f=(v)/(2L)`

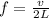
where v is the speed of the wave, L is the length of the string and f is the frequency. Re-arranging the equation and substituting the data of the problem (L=0.90 m and f=256 Hz), we can find v:

`v=2Lf=2(0.90 m)(256 Hz)=460.8 m/s`

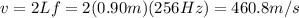
c. 18,000 m

Step-by-step explanation:

The relationship between speed of the wave, distance travelled and time taken is

`v=(d)/(t)`

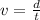
where

v = 6,000 m/s is the speed of the wave

d = ? is the distance travelled

t = 3 s is the time taken

Re-arranging the formula and substituting the numbers into it, we find:

`d=vt=(6,000 m/s)(3 s)=18,000 m`