Question

there are 500 tickets for sale in A raffle. tickets cost $3 each, or $20 for A book of 10. All 500 tickets were sold, and $1350 was raised. How many books of 10 tickets were sold?​

Answer 1

15 booklets of 10 tickets each were sold.

Explanation:

We are given the following information:

Let x be the number of single tickets sold and y be the number of booklets sold.

Each booklet consist of 10 tickets.

There are total of 500 tickets.

Thus, it can be represented by the equation:

`x + 10y =500`

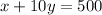
The cost of single ticket = $3

Cost of booklet = $20

Total money raised = $1,350

This, can be represented in the equation:

`3x + 20y = 1350`

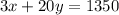
Now, we have obtained two equation in two variable. Solving these equations, we get:

`2x + 20y = 1000\\3x + 20y = 1350\\x = 350\\y = 15`

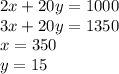
Thus, 15 booklets of 10 tickets each were sold.