Question

NEED HELP ASAAAPPP
PLEASEE IM GOING TO DIEE

Answer 1

1) x² - 6x + 58 = 0

2) x² - 12x + 45 = 0

3) x² - 10x + 23 = 0

4) x² - 2x - 48 = 0

Explanation:

1-4 The form the quadratic equation with its roots:

ax² + -b/a x + c/a = 0 ⇒ b is the sum of the roots and c is the product of the roots.

If the roots are irrational numbers or complex number then they are conjugate

Ex: 1] irrational
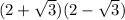`(2+√(3))(2-√(3))` ⇒ their sum and product are

rational numbers

2] complex (5 - 3i)(5 + 3i) ⇒ their sum and product are rational numbers

1) ∵ The first root is 3 + 7i ⇒ ∴ the second root is 3 - 7i

∵ their sum = 3 + 7i + 3 - 7i = 6

∵ their product = (3 + 7i)(3 - 7i) = 9 - 49i² = 9 + 49 = 58⇒(i² = -1)

∴ The equation⇒ x² - 6x + 58 = 0

2) ∵ The first root is 6 - 3i ⇒ ∴ the second root is 6 + 3i

∵ their sum = 6 - 3i + 6 + 3i = 12

∵ their product = (6 - 3i)(6 + 3i) = 36 - 9i² = 36 + 9 = 45⇒(i² = -1)

∴ The equation⇒ x² - 12x + 45 = 0

3) ∵ The first root is 5 + √2 ⇒ ∴ the second root is 5 - √2

∵ their sum = 5 + √2 + 5 - √2 = 10

∵ their product = (5 + √2)(5 - √2) = 25 - 2 = 23

∴ The equation⇒ x² - 10x + 23 = 0

4) ∵ The first root is -6 and the second root is 8

∵ their sum = -6 + 8 = 2

∵ their product = (-6)(8) = -48

∴ The equation⇒ x² - 2x - 48 = 0

5-8 Solving equations:

1) x² - 6x + 58 = 0

a = 1 , b = -6 , c = 58

x =
`\frac{-b+\sqrt{b^(2)-4ac } }{2a}=(--6+√(36-(4)(1)(58)) )/((2)(1))\\ =(6+√(196) )/(2) =(6+14i)/(2)=3+7i`

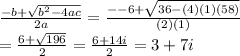
2) x² - 12x + 45 = 0

a = 1 , b = -12 , c = 45

x =
`(--12+√(144-(4)(1)(45)) )/((2)(1))=(12+√(-36) )/(2)\\=(12+6i)/(2)=6+3i`

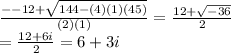
3) x² - 10x + 23 = 0

a = 1 , b = -10 , c = 23

x =
`(--10+√(100-(4)(1)(23)) )/((2)(1))=(10+√(8) )/(2)\\ =(10+2√(2) )/(2)=5+√(2)`

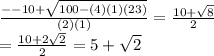
4) x² - 2x - 48 = 0 ⇒ using factorization

(x - 8)(x + 6) = 0

x - 8 = 0⇒ x = 8

x + 6 = 0⇒ x = -6