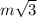The first problem (So is number 3) is a 30-60-90 triangle (The angles add up to 180) but with this combination of numbers, there's a trick to finding the other sides.
Number two is a 45-45-90 triangle, which is also special because knowing that help you find out the lengths. I'll show a picture to explain...
For 45-45-90 triangles, let's use a for the variable. Since these triangles are isosceles two of the legs will be congruent. to find the hypotenuse, the formula is "a" square root 2.
In the diagram, "a" is 9, so then plug in that number and you should get 9 square root 2. You can't simplify it.
For 30-60-90 triangles, let's use "m" as our variable. Your hypotenuse is 2m, the long leg/side is "m" square root 3 and the short leg/ side, that is just "m"
Since we know the length of the hypotenuse, set 2m equal to 24 to get m
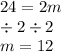
Now that we know "m" plug it into m square root 3