Answer:
D.
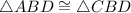 .
.
Explanation:
Given
In triangle ABC a line segment AB is congruent to line segment BC.
Given:
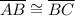
To prove that the base angles of an isosceles triangle are congruent.
i.e

1.Statement: Segment BD is an angle bisector of

Reason: By construction.
2.Statement:

Reason: By definition of an angle bisector.
3.Statement:
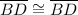
Reason: Reflexive property .
4. Statement:
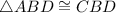
Reason: Side-Angle-Side(SAS)
Postulate
5.Statement:

Reason: CPCT.
Hence proved.