Question

Which of the given functions have an average rate of change of -12 on the interval [0, 2]?

Answer 1

The answer is f(x) = 7 - 12x

Explanation:

f(x) = 7 - 12x has average rate -12 on the interval [0 , 2] because:

f(0) = 7 - 12(0) = 7

f(1) = 7 - 12(1) = -5

f(2) = 7 - 12(2) = -17

The difference between 7 , -5 , -17 is constant and equal -12

∴ The average rate of change is -12

Answer 2

The correct answers are:

1)
`f(x)=-5^x`

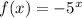
2)
`f(x)=7-12x`

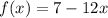
3)
`f(x)=-3(3^x)`

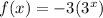
Explanation:

The rate of change of a function in the interval [a,b] is calculated by:

`Rate\ of\ change=(f(b)-f(a))/(b-a)`

We have: [a,b]=[0,2]

1)

`f(x)=-5^x`

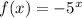
Hence, we have:

`f(2)=-5^2\\\\\\f(2)=-25`

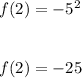
and

`f(0)=-5^0\\\\\\f(0)=-1`

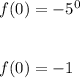
Hence, the rate of change in the interval [0,2] is:

`=(-25-(-1))/(2-0)\\\\\\=(-24)/(2)\\\\\\=-12`

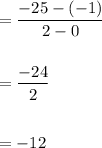
Hence, option: (1) is correct.

2)

`f(x)=7-12x`

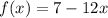
We know that for any linear function of the type y=mx+c

The rate of change in any interval =m

Here we have: m= -12

Hence, Rate of change= -12

Option: 2 is correct.

3)

`f(x)=-3(3^x)`

`f(2)=-3* 3^2\\\\\\f(2)=-27`

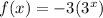
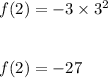
and

`f(0)=-3* 3^0\\\\\\f(0)=-3`

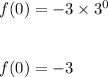
Hence, Rate of change is:

`=(-27-(-3))/(2-0)\\\\\\=(-24)/(2)\\\\\\=-12`

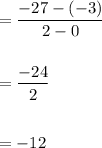
Hence, option: 3 is correct.

4)

`f(x)=-12^x`

`f(2)=-12^2=-144`

`f(0)=-12^0=-1`

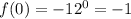
Hence, rate of change is:

`=(-144-(-1))/(2-0)\\\\\\=(-143)/(2)`

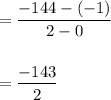
Option: 4 is incorrect.

5)

`f(x)=-(1)/(12)x+9`

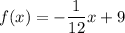
It is linear function.

`Hence\ ,\ rate\ of\ change=(-1)/(12)`

Hence, option: 5 is incorrect.

6)

`f(x)=12x-(2)/(3)`

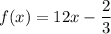
Again it is a linear function with rate of change: 12

Hence, option: 6 is incorrect.