Question

A side of a triangle is divided into three congruent parts. Two lines, parallel to another side of the triangle, are drawn through each dividing point. Find the area of the quadrilaterals formed by those lines if the area of the original triangle is 24.

Answer 1

8 square units and
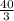`(40)/(3)` square units.

Explanation:

Consider triangle aBc. In this triangle, AD = DF = FB, DE || FG || AC and area of the triangle is 24 square units.

1. Triangles BFG and BAC are similar with the scale factor of 1/3, then

`A_(BFG)=\left((1)/(3)\right)^2 \cdot A_(ABC)=(1)/(9)\cdot 24=(8)/(3)\ un^2.`

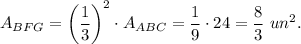
2. Triangles BDE and BAC are similar with the scale factor of 2/3, then

`A_(BDE)=\left((2)/(3)\right)^2 \cdot A_(ABC)=(4)/(9)\cdot 24=(32)/(3)\ un^2.`

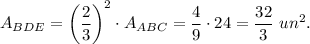
Then the area of the trapezoid DFGE is

`A_(DFGE)=A_(BDE)-A_(BGF)=(32)/(3)-(8)/(3)=8\ un^2.`

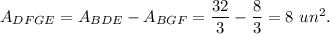
and the area of the trapezoid ADEC is

`A_(ADEC)=A_(ABC)-A_(BDE)=24-(32)/(3)=(40)/(3)\ un^2.`