Answer:
○
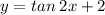
Explanation:
![\displaystyle \boxed{y = -cot\:(2x + (\pi)/(2)) + 2} \\ y = Acot(Bx - C) + D \\ \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (\pi)/(B) \\ Amplitude \hookrightarrow |A| \\ \\ \\ Vertical\:Shift \hookrightarrow 2 \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \hookrightarrow \boxed{-(\pi)/(4)} \hookrightarrow (-(\pi)/(2))/(2) \\ Wavelength\:[Period] \hookrightarrow (\pi)/(B) \hookrightarrow (\pi)/(2) \\ Amplitude \hookrightarrow N/A](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3wt394yfku98xsg6jab6hnmqdkevl4meio.png)
OR
![\displaystyle y = Atan(Bx - C) + D \\ \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (\pi)/(B) \\ Amplitude \hookrightarrow |A| \\ \\ \\ Vertical\:Shift \hookrightarrow 2 \\ Horisontal\:[Phase]\:Shift \hookrightarrow 0 \\ Wavelength\:[Period] \hookrightarrow (\pi)/(B) \hookrightarrow (\pi)/(2) \\ Amplitude \hookrightarrow N/A](https://img.qammunity.org/2020/formulas/mathematics/middle-school/vkct8hy6mnahfrhpb62xd98t59nfy73y0a.png)
Here is all the information you will need. Now, what you need to know is that ALL tangent, secant, cosecant, and cotangent functions have NO amplitudes. Also, keep in mind that although this IS the tangent graph, if you plan on writing your equation as a function of cotangent, then there WILL be a horisontal shift, meaning that a C-term will be involved. As you can see, the red graph displays the trigonometric graph of
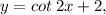 in which you need to replase "tangent" with "cotangent", then figure the appropriate C-term out that will make the graph horisontally shift and map onto the tangent graph [graph in blue], accourding to the horisontal shift formula above. Also keep in mind that the −C gives you the OPPOCITE TERMS OF WHAT THEY REALLY ARE, so you must be careful with your calculations. So, between the two graphs, we can tell that the cotangent graph [graph in red] is shifted
in which you need to replase "tangent" with "cotangent", then figure the appropriate C-term out that will make the graph horisontally shift and map onto the tangent graph [graph in blue], accourding to the horisontal shift formula above. Also keep in mind that the −C gives you the OPPOCITE TERMS OF WHAT THEY REALLY ARE, so you must be careful with your calculations. So, between the two graphs, we can tell that the cotangent graph [graph in red] is shifted
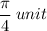 to the right, which means that in order to match the tangent graph [graph in blue], we need to shift the graph BACKWARD
to the right, which means that in order to match the tangent graph [graph in blue], we need to shift the graph BACKWARD
 which means the C-term will be negative, and perfourming your calculations, you will arrive at
which means the C-term will be negative, and perfourming your calculations, you will arrive at
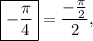 but we are NOT YET DONE. Although we shifted the graph back into position, remember, cotangent is graphed in REVERCE, so we need to insert a negative in front of the amplitude term, and with that, the cotangent graph of the tangent graph, accourding to the horisontal shift, is
but we are NOT YET DONE. Although we shifted the graph back into position, remember, cotangent is graphed in REVERCE, so we need to insert a negative in front of the amplitude term, and with that, the cotangent graph of the tangent graph, accourding to the horisontal shift, is
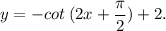
I am delighted to assist you at any time.