Question

Given ​ f(x) = x^2 − 2x − 5​.

Enter the quadratic function in vertex form in the box.

Answer 1

`(x - 1)^2 - 6`

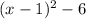
Explanation:

You need to know:

Vertex form =
`a(x -h)^2 + k`

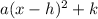
The vertex is at

(h, k)

Need to know about perfect squares

Need to know how to complete the square.

-----------------------------------------------------------------------------------------

To convert
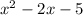`x^2-2x-5` you need to complete the square on the equation.

Complete the Square
`x^2 - 2x -5`

`x^2 - 2x -5`

`(x^2 - 2x) -5`

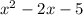
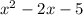
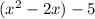
Divide -2 by 2 and then square it.

`(-2)/(2) = -1`

`-1^2 = 1`

Add the one to the parentheses and subtract the one from the 5

`(x^2 - 2x +1) -5 -1`

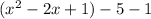
Square
`(x^2 - 2x +1)`

`(x-1)^2`

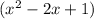
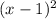
Now we have

`(x - 1)^2 -5 -1`

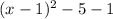
Next add -5 - 1 = -6

`(x - 1)^2 - 6`

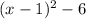
Our quadratic is in vertex form now.

Vertex form =
`a(x -h)^2 + k`

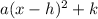
our equation =
`(x - 1)^2 - 6`

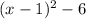
Vertex = (1, -6)