Question

Given: △KLM, KM=48, LD=16
LD⊥KM, NOPS - rectangle NO:OP=5:9 Find: NO, OP

Answer 1

NO = 10 and OP = 18

Explanation:

Given: KM = 48 , LD = 16 , NO : OP = 5 : 9 and NOPS is rectangle.

To find: Value of NO and OP

Let the value of NO and OP = 5x and 9x

frst we prove ΔKLD is similar to ΔKON and ΔMLD is similar to ΔMPS

In ΔKLD and ΔKON

∠KDL = ∠KNO = 90° ( corresponding angles )

∠DKL = ∠NKO ( common Angle )

⇒ ΔKLD is similar to ΔKON by AA similarity rule.

⇒
`(KD)/(KN)=(LD)/(ON)`

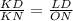
subtract 1 from both sides

⇒
`(KD)/(KN)-1=(LD)/(ON)-1`

⇒
`(KD-KN)/(KN)=(LD-ON)/(ON)`

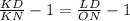
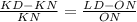
by substituting value from figure,

⇒
`(ND)/(KN)=(16-5x)/(5x)`

⇒
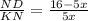
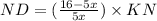`ND=((16-5x)/(5x))* KN` ..................... (1)

In ΔMLD and ΔMPS

∠MDL = ∠MSP = 90° ( corresponding angles )

∠DML = ∠SMP ( common Angle )

⇒ ΔMLD is similar to ΔMPS by AA similarity rule.

⇒
`(MD)/(SM)=(LD)/(PS)`

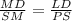
subtract 1 from both sides

⇒
`(MD)/(SM)-1=(LD)/(PS)-1`

⇒
`(MD-SM)/(SM)=(LD-PS)/(PS)`

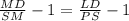
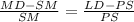
by sustituting value from figure,

⇒
`(DS)/(SM)=(16-5x)/(5x)`

⇒
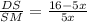
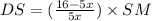`DS=((16-5x)/(5x))* SM` ..................... (2)

Add eqn. (1) & (2), we get

`ND+DS=((16-5x)/(5x))* KN + ((16-5x)/(5x))* SM`

`NS=((16-5x)/(5x))(KN+SM)`

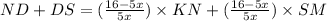
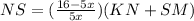
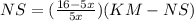`NS=((16-5x)/(5x))(KM-NS)` ( from figure KN + SM = KM - NS)

substitute given values,

`9x=((16-5x)/(5x))(48-9x)`

`9x * 5x=16*48+16*(-9x)-5x*48-5x*(-9x)`

`45x^2=768-144x-240x+45x^2`

`45x^2-45x^2=768-384x`

`768-384x=0`

`384x=768`

`x=(768)/(384)`

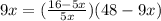
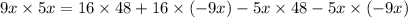
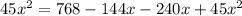
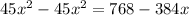
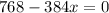
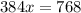
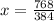
x = 2

⇒ NO = 5x = 5 × 2 = 10

⇒ OP = 9x = 9 × 2 = 18