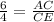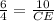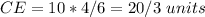Question

PLEASE HELP IF POSSIBLE!!

4. Which similarity postulate or theorem proves the triangles are similar? (1 point)

5. What are the congruent angles and/or proportional segments that justify the answer in number 4?

Note- Picture is attached and the answer IS NOT the hypotenuse leg theorem

Answer 1

Part 4) AA Similarity Postulate

Part 5)

The congruent angles are

m<ACB=m<CED , m<ABC=m<CDE, m<BAC=m<DCE

The proportional segments are

`(AB)/(DC)=(BC)/(DE)=(AC)/(CE)`

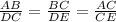
Explanation:

Part 4) we know that

If BC is parallel to DE

then

Triangles ABC and CDE are similar by AA Similarity Postulate ( the three interior angles are congruent)

so

m<ACB=m<CED ------> by corresponding angles

m<ABC=m<CDE -----> both angles measure is 90 degrees

m<BAC=m<DCE -----> the sum of the interior angles of a triangle must be equal to 180 degrees

If two figures are similar, then the ratio of its corresponding sides is equal

so

`(AB)/(DC)=(BC)/(DE)=(AC)/(CE)`

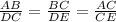
substitute the values

`(6)/(4)=(8)/(DE)=(AC)/(CE)`

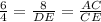
Find DE

`(6)/(4)=(8)/(DE)`

`DE=8*4/6=16/3\ units`

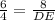
In the triangle ABC

Applying Pythagoras Theorem

Find AC

`AC^(2)=AB^(2)+BC^(2)`

`AC^(2)=6^(2)+8^(2)`

`AC^(2)=100`

`AC=10\ units`

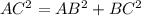
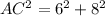
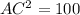
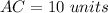
Find CE

`(6)/(4)=(AC)/(CE)`

`(6)/(4)=(10)/(CE)`

`CE=10*4/6=20/3\ units`