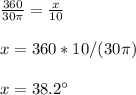Question

What is the approximate measure, in degrees, of the central angle of the circle whose radius is 15 m and arc length is 10 m?

Answer 1

`38.2\°`

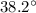
Explanation:

we know that

The circumference of a circle is equal to

`C=2\pi r`

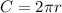
we have

`r=15\ m`

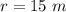
substitute

`C=2\pi (15)=30\pi\ m`

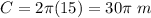
Remember that

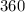`360` degrees subtends the complete circle of length
`30\pi\ m`

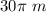
so

by proportion

Find the approximate measure, in degrees, of the central angle of the circle whose radius is 15 m and arc length is 10 m

so

`(360)/(30\pi)=(x)/(10)\\ \\x=360*10/(30\pi)\\ \\x=38.2\°`