Answer:
Part 1) The minimum value is
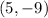
Part 2) The x-intercepts are -2 and 5
Part 3) The zeros of the function are -9 and -8
Part 4) The minimum value is
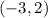
Explanation:
Part 1) we have
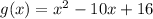
we know that
The equation of a vertical parabola in vertex form is equal to
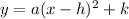
where
(h,k) is the vertex
if a>0---> the the parabola open upward (vertex is a minimum)
If a<0---> the the parabola open downward (vertex is a maximum)
Convert to vertex form
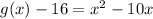
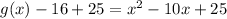
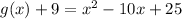
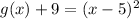
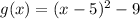 ------> vertex form
------> vertex form
The vertex is the point
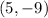
the parabola open upward (vertex is a minimum)
Part 2) we have
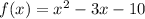
we know that
The x-intercepts are the values of x when the value of the function is equal to zero
so
equate the equation to zero
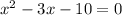
The formula to solve a quadratic equation of the form
 is equal to
is equal to

in this problem we have
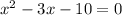
so
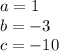
substitute in the formula

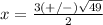
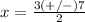
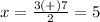
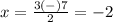
Part 3) we have
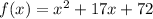
we know that
The zeros of the function are the values of x when the value of the function is equal to zero
so
equate the equation to zero
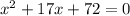
The formula to solve a quadratic equation of the form
 is equal to
is equal to

in this problem we have
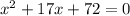
so
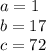
substitute in the formula
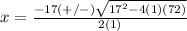
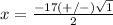
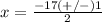
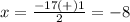
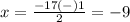
Part 4) we have
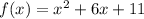
we know that
The equation of a vertical parabola in vertex form is equal to
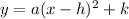
where
(h,k) is the vertex
if a>0---> the the parabola open upward (vertex is a minimum)
If a<0---> the the parabola open downward (vertex is a maximum)
Convert to vertex form
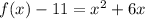
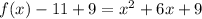
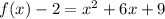
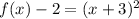
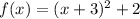
The vertex is the point
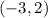
the parabola open upward (vertex is a minimum)