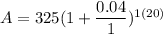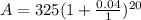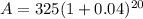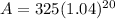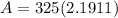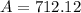Answer:
338 (1 Year)
365.58 (3 Years)
427.68 (7 Years)
712.12 (20 Years)
Explanation:
To find the compounded annual value, we use the formula:
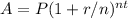
Let's first take each variable and list them:
P = 325
r = 4% or 0.04
t = 1, 3, 7, 20
n = 1
Let's take each number of years one at a time.
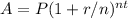
After 1 Year
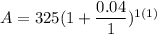
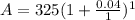
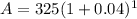
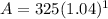
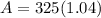
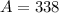
After 3 Years
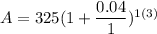
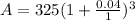
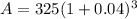
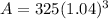
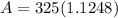
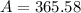
After 7 Years
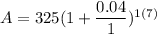
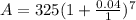
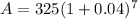
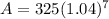
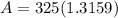
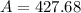
After 20 years