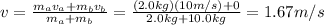Question

A 2.0 kg arrow is fired at 10 m/s into a stationary 10kg block of ice what is the velocity of the arrow / ice combination after the collision?

Answer 1

1.67 m/s

Step-by-step explanation:

Since this is an inelastic collision (the block and the arrow stick together after the collision), we can solve the problem by using the law of conservation of momentum:

`p_i = p_f\\m_a v_a + m_b v_b = (m_a + m_b) v`

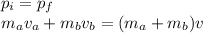
where

`m_a = 2.0 kg` is the mass of the arrow

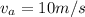`v_a = 10 m/s` is the initial speed of the arrow

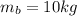`m_b = 10 kg` is the mass of the block

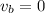`v_b = 0` is the initial speed of the block

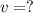`v = ?` is the final speed of the arrow+block

Substituting and re-arranging the equation, we find:

`v=(m_a v_a + m_b v_b)/(m_a +m_b)=((2.0 kg)(10 m/s)+0)/(2.0 kg+10.0 kg)=1.67 m/s`