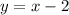Answer:
True. The slant asymptote is
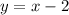
Explanation:
A slant asymptote is the equation of a line of the form y = mx + b
Where m is the slope and b is the cut point with the y axis.
To find these asymptotes, you must make the following limit:
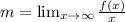
![b = \lim_(x \to \infty)[f(x) -mx]](https://img.qammunity.org/2020/formulas/mathematics/high-school/qwydxu0870c3fqm2yi2r2qx132idp9nypl.png)
With the given function f(x) we make the first limit to find the slope of the line:
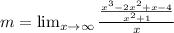

We divide each term between
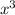
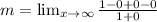

Now we solve the second limit
![b = \lim_(x \to \infty)[(x^3-2x^2+x-4)/(x^2+1)-x]\\\\b = \lim_(x \to \infty)[(x^3-2x^2+x-4 -[x^3+x])/(x^2+1)]\\\\b = \lim_(x \to \infty)[(-2x^2-4)/(x^2+1)]\\\\b = \lim_(x \to \infty)[(-2(x^2)/(x^2)-(4)/(x^2))/((x^2)/(x^2)+(1)/(x^2))]\\\\\\b = -2](https://img.qammunity.org/2020/formulas/mathematics/high-school/m2k37gxah7kk5m28uvrylyjsphe0d38p0y.png)
Finally: The slant asymptote is