Question

Find the constant of variation for the relation and use it to write an equation for the statement. Then solve the equation.

If y varies directly as x, and y=7 when x=3, find y when x=7

Answer 1

choice a is correct.

Explanation:

As y varies directly as x so we can write y = kx.

Here k is constant of proportionality.

First we find the value of k.

We use the values of x and y to find the value of k.

y = 7 when x = 3

y = kx

7 = k(3)

7/3 = k

k = 7/3

Hence y = 7/3x

Now, we have to find the value of y when x = 7

y = 7/3(7)

y = 49/3

Answer 2

Option a is correct

Explanation:

Given that y varies directly as x

Hence y can be written as kx

y=kx where k is the constant of proportionality

To find k:

Use the fact that y=7 when x=3

We get

7 =3k

OR k =
`(7)/(3)`

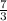
Hence the relation between x and y is

`y=(7)/(3)x`

To find y value when x=7:

From the relation we found we substitute x =7 to find y

`y=(7)/(3) (7)=(49)/(3)`

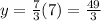
Option a is correct