Question

Use the graph that shows the solution to F(x) = G(x)

F(x) = 7/3x-3
G(x) =2^x - 4
What is the solution to f (x) = g(x)
Select each correct answer
A -1/2
B 0
C 2
D 3

Answer 1

Option (b) and (d) is correct.

The solution where f (x) = g(x) is when x = 0 and x = 3

Explanation:

Given : functions
`F(x) = (7)/(3)x-3` and
`G(x) =2^x-4`

We have to find the solution where f (x) = g(x)

Consider the given function
`F(x) = (7)/(3)x-3` and
`G(x) =2^x-4`

The solution where f (x) = g(x) is the point where both graph intersect at y- axis.

Then it is seen clearly from graph of both the functions intersect at point (0, -3) and (3,4)

When x = 0 both f(0) and g(0) = -3

When x = 3 both f(3) and g(3) = 4

Thus, the solution where f (x) = g(x) is when x= 0 and x= 3

Thus, Option (b) and (d) is correct.

Answer 2

Answer: B. 0 and D. 3

Explanation:

Here the given function is,

`f(x) = (7)/(3)x-3`

`g(x) = 2^x-4`

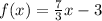
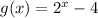
For finding the solution of this system of equation,

First we will plot the function on the graph,

Graph of function f(x),

x-intercept and y-intercept are (1.286,0) and (0,-3) respectively,

Also, it is a straight line,

Hence, we can plot this line on the graph,

Graph of function g(x),

Function g(x) is an exponential function having x-intercept and y -intercept, (2,0) and (0,-3) respectively.

Also, the end behavior is,

As
`x\rightarrow \infty` ,
`f(x)\rightarrow \infty`

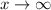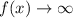
As
`x\rightarrow -\infty` ,
`f(x)\rightarrow -4`

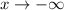Hence, we can plot the graph of g(x),

By plotting the graph,

We found that the intersection of the function f(x) and g(x) are (0,-3) and (3,4).

Hence, the solution of the system is the x-coordinates of the intersection points that are 0 or 3.

⇒ Option B and C is the correct options.