Answer:
option (b) is correct.
the solution to f(x) = G(x) is at x = 0
Explanation:
Given :
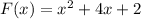 and
and
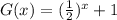
We have to find the solution for which f(x) = G(x)
for given two functions
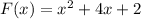 and
and
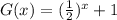 the solution where f(x) = G(x) is the point where two graphs meets.
the solution where f(x) = G(x) is the point where two graphs meets.
that is the point of intersection .
From graph it is clear that point (0, 2)
That is when x = 0 then value of both functions f(x) and g(x) is 2.
Thus, option (b) is correct.
Thus, the solution to f(x) = G(x) is at x = 0