Answer:
Option b is correct
 .
.
Explanation:
Domain is the set of all possible values of x where function is defined.
Given the function:
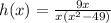
To find the domain of the given function:
Exclude the values of x, for which function is not defined
Set denominator = 0
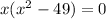
By zero product property;
 and
and
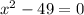
⇒x = 0 and
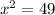
⇒x = 0 and
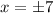
Therefore, the domain of the given function is:
