Question

Help me asap. thanks

Answer 1

Option C is correct.

Explanation:

An exponential is in the form of :

`f(x) = ab^x`

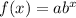
where

a is the initial value and

b is the growth factor.

If b> 1 , then the graph is increasing.

if 0<b<1, then the graph is decreasing.

Given the function:

`f(x) = 2^(x+3)`

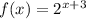
we can write this as:

`f(x) = 2^x \cdot 2^3 = 8 \cdot 2^x`

⇒
`f(x) =8 \cdot (2)^x`

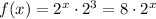
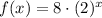
Here, b = 2 > 1

y-intercept: The graph crosses the y-axis

Substitute x = 0 and solve for f(x):

`f(0) =8 \cdot (2)^0`

⇒
`f(0) = 8`

⇒
`a = 8`

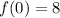
Graph of this function:

We make table for some values of x;

x f(x)

-1 4

0 8

1 16

2 32

Note as x increase, f(x) increases

Now, plot these points on the coordinate plane.

You can see the graph of the given function shown below.

Answer 2

The third graph is the graph of the function provided

Explanation:

A simple technique that can be used to identify the graph that matches the given function is; determination of the y-intercept and then using elimination method to match the function with its graph. At the y-intercept the value of x is always zero, so we replace x with zero in the right hand side of the equation; y(x) = 2^(0+3) = 8. The graph of the function should therefore cross the y-axis at the point (0,8). Thus, the third graph is the graph of the given function.