Question

Which of the following solutions to the equation below x^2+4x-9=5x+3

Answer 1

x^2+4x-9=5x+3

answer= 4 and -3

Answer 2

The correct options are D and E.

Explanation:

The given equation is

`x^2+4x-9=5x+3`

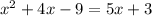
Subtract 5x+5 from both the sides.

`x^2+4x-9-5x-3=0`

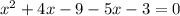
Combine like terms.

`x^2-x-12=0`

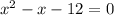
The middle term can be written as -4x+3x.

`x^2-4x+3x-12=0`

`x(x-4)+3(x-4)=0`

`(x-4)(x+3)=0`

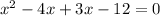
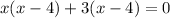
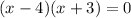
Using zero product property, equate each factor equal to 0.

`x-4=0\Rightarrow z=4`

`x+3=0\Rightarrow z=-3`

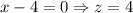
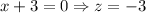
Therefore correct options are D and E.