Question

Arc measures and arc lengths , could you show work also

Answer 1

17. Arc AB has a measure of 90 degrees. This means the angle subtending this arc (angle APB) is a right angle, and so triangle PAB is is a right triangle. The sides of the triangle AP and BP have length equal to the radius of the circle. By the Pythagorean theorem,

`AP^2+BP^2=AB^2\implies AB=√(3^2+3^2)=3\sqrt2`

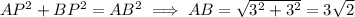
so the answer is A.

20. To find the measure of arc AUB, we need to find the measure of the central angle AQB. This angle is part of the quadrilateral AQBP, which is a kite because we're given that PQ and AB are perpendicular.

Arc AVB has measure 60 degrees, so the central angle subtending it (angle APB) also has measure 60 degrees. PQ bisects this angle, so angle APQ has measure 30 degrees.

QA is tangent to circle P, so angle PAQ is a right angle. The sum of the measuers of the interior angles of any triangle is 180 degrees, so

`m\angle APQ+m\angle PAQ+m\angle AQP=180^\circ\implies m\angle AQP=60^\circ`

PQ also bisects the angle AQB, so that
`m\angle AQB=2m\angle AQP`, and therefore the angle AQB has measure 120 degrees, which in turn is the measure of arc AUB.