Question

Use the identity (x2+y2)2=(x2−y2)2+(2xy)2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6.

Enter your answer as a number, like this: 42

Answer 1

(x²+y²)² = 169

Explanation:

We have given that

The difference of the squares of the numbers is 5.

x²-y² = 5

The product of the numbers is 6.

xy = 6

We have to find the sum of the squares of two numbers.

x²+y² = ?

We have given following formula:

(x²+y²)² = (x²-y²)²+(2xy)²

(x²+y²)² = (5)²+4(6)²

(x²+y²)² = 25+4(36)

(x²+y²)² = 25+144

(x²+y²)² = 169 which is the answer.

Answer 2

The sum of the squares of two numbers whose difference of the squares of the numbers is 5 and the product of the numbers is 6 is 169

Explanation:

Given : the difference of the squares of the numbers is 5 and the product of the numbers is 6.

We have to find the sum of the squares of two numbers whose difference and product is given using given identity,

`(x^2+y^2)^2=(x^2-y^2)^2+(2xy)^2`

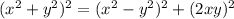
Since, given the difference of the squares of the numbers is 5 that is
`(x^2-y^2)^2=5`

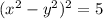
And the product of the numbers is 6 that is
`xy=6`

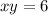
Using identity, we have,

`(x^2+y^2)^2=(x^2-y^2)^2+(2xy)^2`

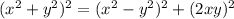
Substitute, we have,

`(x^2+y^2)^2=(5)^2+(2(6))^2`

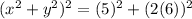
Simplify, we have,

`(x^2+y^2)^2=25+144`

`(x^2+y^2)^2=169`

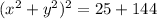
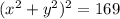
Thus, the sum of the squares of two numbers whose difference of the squares of the numbers is 5 and the product of the numbers is 6 is 169