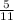Answer:

Explanation:
If P(x) is a polynomial and we have to find all the potential rational roots of P(x) , we take all the possible ratios of the factors of "leading coefficient and the "constant term".
If
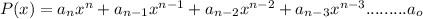
Possible Rational Roots
=±factors of
 /factors of
/factors of
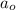
Here in our polynomial
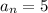
factors of 5 = 1 , 5
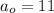
factors of 11 = 1,11
Hence possible rational roots are
±factors of 5 / factors of 11
±
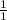 , ±
, ±
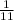 , ±
, ±
 , ±
, ±