2 Answers

Ezequiel Muns · Answer 1 · 2020-03-20T02:20:18+0000

For this case, we chose two points through which the line passes and we find the slope of it, knowing that the cut point with the y axis is 2.

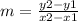
$m = \frac {y2-y1} {x2-x1}$

The chosen points are:

(0.2)

(-4.0)

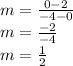
$m = \frac {0-2} {- 4-0}\\m = \frac {-2} {- 4}\\m = \frac {1} {2}$

The line is given by:

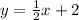
$y = \frac {1} {2} x + 2$

We evaluate a point of the shaded region in each one of the options to know which one is fulfilled.

We choose the point (x, y) = (2,1)

Option A:

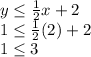
$y \leq \frac {1} {2} x + 2\\1 \leq \frac {1} {2} (2) +2\\1 \leq 3$

If it is fulfilled.

Option B:

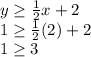
$y\geq \frac {1} {2} x + 2\\1\geq \frac {1} {2} (2) +2\\1\geq 3$

It is not fulfilled

Answer:

Option A

Please log in or register to add a comment.