Answer:
Length of the Rectangle is to be considered as the circumference of the resulting cylinder and the width of the rectangle should be considered as the height of the cylinder only then we get the maximum volume of the cylinder which is 47.77
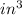
Explanation:
The given dimensions are
Width of the rectangle is 6inches.
Length of the rectangle 10inches.
Now we need to choose in what orientation we need to use the length and the width of the rectangle so that it can be rolled into a rectangle and we get the maximum volume of the resulting cylinder.
so lets consider two cases
CASE-1: width of the rectangle is to be rolled as the circumference of the cylinder and length of the rectangle is to used as the height of the cylinder
2*pi*r = 6
r =
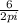
r =
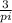 Inch
Inch
and the height = 10inch.
Volume of the resultant cylinder will be
=
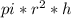
=
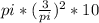
=
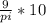
=
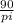 = 28.662
= 28.662
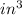
CASE-2: When the length of the rectangle is to used as the circumference of the resultant cylinder and the width of the cylinder is used as the height of the cylinder.
2*pi*r= 10
r =
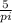
and the height of the cylinder is 6 inch
Now the volume of the cylinder will be
Volume=
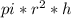
=
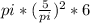
=
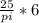
=
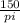 = 47.77
= 47.77
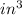
Clearly we have the second case in which the resulting Cylinder will have the maximum volume.
Therefore the CASE-2 will provide the maximum Volume of 47.77
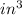 to the resulting cylinder in which the length of the rectangle is to be considered as the circumference of the Cylinder and the width of the rectangle is to be considered as the height of the cylinder.
to the resulting cylinder in which the length of the rectangle is to be considered as the circumference of the Cylinder and the width of the rectangle is to be considered as the height of the cylinder.