Answer:
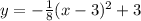
Step-by-step explanation:
Assume a general point (x,y) that belong to the curve
To get the equation of the parabola, we follow the given steps:
1- Find the distance between point (x,y) and the focus point:
The general point is (x,y) and the focus is (3,1)
Using the distance formula:
D =
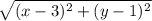 .................> equation I
.................> equation I
2- Find the distance between the point (x,y) and the directrix:
Directrix is a horizontal line having the general equation y=c
We are given that the directrix is y = 5
Therefore, the distance between the point and the directrix will simply be:
|y-c| = |y-5| ...............> equation II
3- Equate equations I and II and solve for y:
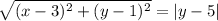
a- Square both sides:
(x-3)² + (y-1)² = (y-5)²
b- Now, expand the brackets having y:
(x-3)² + y² - 2y + 1 = y² - 10y + 25
c- Finally, solve for y:
(x-3)² + 1 - 25 = -10y + 2y
(x-3)² - 24 = -8y
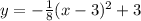
Attached is the graph for the parabola.
Hope this helps :)