Question

Peanut allergies among children. About 2% of children in the United States are allergic to peanuts. Choose three children at random and let the random variable XX be the number in this sample who are allergic to peanuts. The possible values XX can take are 0, 1, 2, and 3.

What is the conditional probability that exactly two of the children will be allergic to peanuts, given that at least one of the three children suffers from this allergy?

(Round your answer to six decimal places.)

P(X=2|X⩾1)P(X=2|X⩾1) =

Answer 1

P(X=2|X≥1) = 0.0199973.

Explanation:

The chance that each of the three children is allergic to peanuts is independent. Each with a chance of 2% = 0.02.

X follows a binomial distribution with

• 3 trials, and
• a chance of "success" of 2% = 0.02.

`P(X = 2|X\ge 1) = (P(X = 2 \cap X\ge 1))/(P(X\ge 1))`.

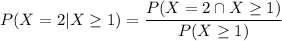The event
`X \ge 1` includes

• 
  `X = 1`
• 
  `{\bf X = 2}`, and
• 
  `X = 3`.

In other words,
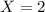`X = 2` implies that
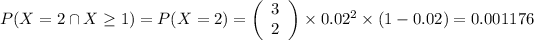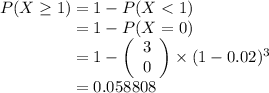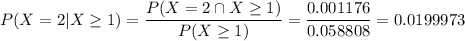`X\ge 1`.

`P(X = 2 \cap X\ge 1) = P(X = 2) = \left(\begin{array}{c}3\\2\end{array}\right ) * 0.02^(2) * (1-0.02) = 0.001176`.

`P(X\ge 1) = 1 - P(X< 1) \\\phantom{P(X\ge 1)}= 1 - P(X = 0) \\\phantom{P(X\ge 1)}= 1 -\left(\begin{array}{c}3\\0\end{array}\right ) * (1-0.02)^(3) \\\phantom{P(X\ge 1)}= 0.058808`.

`P(X = 2|X\ge 1) = (P(X = 2 \cap X\ge 1))/(P(X\ge 1)) = (0.001176)/(0.058808) = 0.0199973`.