Answer:
![16\sqrt[3]{-1}](https://img.qammunity.org/2020/formulas/mathematics/high-school/btvrmhhq16lo0mbet6p76eycygrgxf20p7.png)
Explanation:
Given complex numbers:
z1 = 8(cos20° + isin20°)
z2 = 2(cos40° + i sin40°)
z1.z2 = 8(cos20° + isin20°) * 2(cos40° + i sin40°)
Converting degree to radians:
8(cos(π/9) + isin(π/9)) * 2(cos(2π/9) + i sin(2π/9))
Use the following identity:
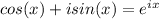
8(cos(π/9) + isin(π/9)) * 2(cos(2π/9) + i sin(2π/9)) will become:
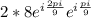
=
![16\sqrt[3]{-1}](https://img.qammunity.org/2020/formulas/mathematics/high-school/btvrmhhq16lo0mbet6p76eycygrgxf20p7.png)