Answer:
Quotient is i/3.
Explanation:
Given:
Complex numbers are 3( cos 135° + i sin 135° ) and 9( cos 45° + i sin 45° )
To find: Quotient of the given complex number.
Consider,
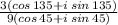
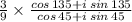
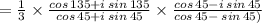
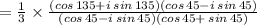
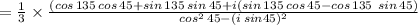
using, cos A cos B + sin A sin B = cos( A - B ) and sin A cos B - cos A sin B = sin( A - B )
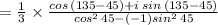
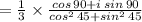
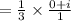
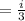
Therefore, Quotient is i/3.