Question

Which of the following expressions is equal to g(x)?

Answer 1

d is the right choice on plato

Explanation:

Answer 2

Option D is right

Explanation:

Given are two graphs. The first one is given as

`f(x) = log_(2) x\\`

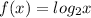
The second one equation we have to find out.

Option A given as

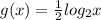`g(x) =(1)/(2)  log_(2) x` is having x intercept as

(0,1/2). But our g(x) has x intercept as 1. Hence not correct.

Option B:
`g(x) = log_(2) (1)/(2) x`

This has x intercept as (0,2). Since does not match with g(x) not correct

OPtion C:

`g(x) = log_(2) 2x`

Here x intercept = 1 matches with ours.

Also g(2) = 2, twice as that of original f(x)

Hence option C is not right

Option D is only right because x intercept should be 1 and also when x=4 y=2(log 4 to base 2)