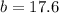Question

Find all solutions for a triangle with A=40 degrees , B=60 degrees and c = 20.

Answer 1

bc a triangle has a total of 180°, add angles A+B to get 40+60=100, so angle C must be 80° since 180°-100°= 80°

then use sohcahtoa

Answer 2

The correct option is C)
`\angle C=80\degree` ,
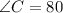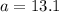`a=13.1` and
`b=17.6`

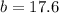
Explanation:

We need to calculate the solution for a triangle with
`A=40\degrees \, B=60\degrees \ and \ c = 20`

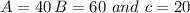
Since, interior angle sum of triangle is 180°

`\angle A +\angle B +\angle C=180\degree`

`40\degree + 60\degree +\angle C=180\degree`

`100\degree +\angle C=180\degree`

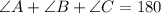
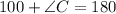
Subtract both the sides by
`100\degree`

`\angle C=180\degree-100\degree`

`\angle C=80\degree`

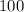
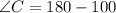
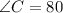
Sine law:-

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

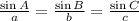
by sine law

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

`(\sin 40\degree)/(a)=(\sin 60\degree)/(b)=(\sin 80\degree)/(20)`

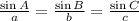
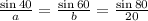
Compare first and third fractions,

`(\sin 40\degree)/(a)=(\sin 80\degree)/(20)`

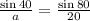
cross multiply

`(20 \sin 40\degree)/(\sin 80\degree)=a`

`(20* 0.642)/(0.984)=a`

`a=13.1`

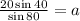
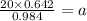
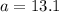
Compare second and third fractions,

`(\sin 60\degree)/(b)=(\sin 80\degree)/(20)`

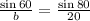
cross multiply

`(20 \sin 60\degree)/(\sin 80\degree)=b`

`(20* 0.866)/(0.984)=b`

`b=17.6`

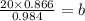
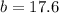
Hence, the correct option is C)
`\angle C=80\degree` ,
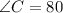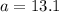`a=13.1` and
`b=17.6`