Answer:
Volume cylinder = 24501.42 m³
The surface area of the cone = 151.5 in²
The lateral area of the square pyramid = 352 in²
Explanation:
∵ The volume of the cylinder = area base × height
∵ Its base is a circle
∴ V = πr² × h = 3.14 × (34/2)² × 27 = 24501.42 m³
∵ The surface area of the cone = 1/2 perimeter base × Slant height + area base
∵ Its base is a circle
∴ S.A = (1/2) × 2πr × l + πr²
∵ The slant height =
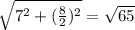
∴ S.A = 3.14 × (8/2) × √65 + 3.14 × (8/2)² = 151.5 in²
∵ The lateral area of the square pyramid = 1/2 perimeter base × slant height
∵ Its base is a square
∴ L.A = 1/2 × (8 × 4) × 22 = 352 in²