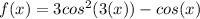Question

I require some math assistance please.

Answer 1

The correct answer is C

Explanation:

The easiest way to check is to use the definition of an even function;

If a function is even, then

`f(a)=f(-a)`

The sine function and its inverse are odd functions.

The tangent function is also an odd function.

Let us verify this definition for the cosine function.

Let

`f(x)=3\cos^2(3x)-\cos(x)`

Then

`f(a)=3\cos^2(3a)-\cos(a)`

Also,

`f(-a)=3\cos^2(-3a)-\cos(-a)`

Recall that;

`\cos(-\theta)=\cos(\theta)`

`f(-a)=3\cos^2(3a)-\cos(a)`

Hence;

`f(a)=f(-a)`

The correct answer is C.

If you try this for;

`f(x)=2sin^2(4x)+5sin(x)`

We will obtain;

`f(a)=2sin^2(4a)+5sin(a)`

and

`f(-a)=2sin^2(-4a)+5sin(-a)`

Recall that;

`\sin(-\theta)=-\sin(\theta)`

This implies that;

`f(-a)=-2sin^2(4a)-5sin(a)`

Hence;

`f(a) \\e f(-a)`

The same thing applies to the tangent function as well as the co-secant function.

Answer 2

Option C.

Explanation:

By definition, a function f(x) is even if
`f(-x) =f(x)`

We know by definition that the function sin(x) is odd and the function cos(x) is even.

With this information we can analyze each function and find out which is even.

A. The first function is not even because 5sin(x) is an odd function.

B. The second function is not even because 2tan(x) is not an even function.

C. The third function is even, because -cos(x) and
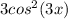`3cos^2(3x)` are even functions.

`f(-x) = 3cos^2(3(-x)) - cos(-x) = 3cos^2(3(x)) - cos(x) = f(x)`

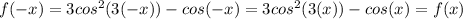
D. The fourth function is not even because csc(x) is not an even function.

Therefore the correct answer is the option C.
`f(x)=3cos^2(3(x)) - cos(x)`