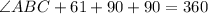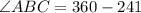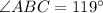Answer:
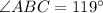
Length of DC= 105 feet.
Step-by-step explanation:
Given
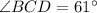
Right trapezoid means two angle are of 90 degree.


Draw a perpendicular BE and BE
 AD .
AD .
Length of AB=80 feet
Length of BC=65 feet
Length of AD=60 feet
Length of DC= DE+ EC
Let length of EC= x
Quadrilateral ABED is a parallelogram
 AB
AB
 DE and AB= DE=80 feet
DE and AB= DE=80 feet
AD= BE=60 feet
Therefore, Length of DC= 80+x
In

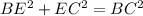
By using pythogorous theorem
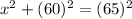
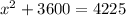
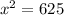
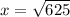
x=25
Therefore, length of DC= DE+EC=80+25=105 feet .
In quadrilateral ABCD
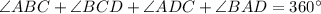
By usnig property of sum of angles of quadrilateral