Question

What is the value of the shown image?

Answer 1

Option B. 7 is the correct answer.

Explanation:

The given expression is
`\sum_(t=1)^(3)[{4* ((1)/(2))^(t-1)}]`

Now by putting the the values of t = 1, 2, 3 we get the sequence.

Then we can add the terms of the sequence

First term =
`4.((1)/(2))^(1-1) = 4.1 = 4`

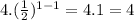
Second term =
`4.((1)/(2))^(2-1)=4.((1)/(2)) = 2`

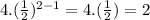
Third term =
`4.((1)/(2))^(3-1)=4.((1)/(2))^(2)=4.(1)/(4)=1`

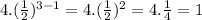
So the total of these terms will be = 4 + 2 + 1 = 7

Answer is 7.

Answer 2

Option B

Explanation:

To solve the problem you must develop the sum shown.

Note that the sum goes from i = 1 to i = 3.

Therefore they ask you to make the following sum

`4(0.5) ^ {1-1} + 4(0.5) ^ {2-1} + 4(0.5) ^ {3-1}`

Simplifying, we have:

`4(0.5) 0 + 4(0.5) 1 + 4(0.5)^ 2\\\\4(1) + 4(0.5) + 4(0.25)\\\\4 + 2 + 1 = 7`.

The answer is option B