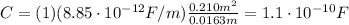Question

A parallel-plate air capacitor is made from two plates 0.210 m square, spaced 0.815 cm apart. it is connected to a 120 v battery. if the plates are pulled apart to a separation of 1.63 cm , suppose the battery remains connected while the plates are pulled apart. part a what is the capacitance?

Answer 1

at the beginning:
`2.3\cdot 10^(-10) F`

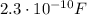
when the plates are pulled apart:
`1.1\cdot 10^(-10) F`

Step-by-step explanation:

The capacitance of a parallel-plate capacitor is given by

`C=k \epsilon_0 (A)/(d)`

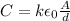
where

k is the relative permittivity of the medium (for air, k=1, so we can omit it)

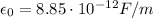`\epsilon_0 = 8.85\cdot 10^(-12) F/m` is the permittivity of free space

A is the area of the plates of the capacitor

d is the separation between the plates

In this problem, we have:

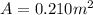`A=0.210 m^2` is the area of the plates

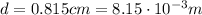`d=0.815 cm=8.15\cdot 10^(-3) m` is the separation between the plates at the beginning

Substituting into the formula, we find

`C=(1)(8.85\cdot 10^(-12)F/m)(0.210 m^2)/(8.15\cdot 10^(-3) m)=2.3\cdot 10^(-10) F`

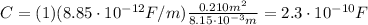
Later, the plates are pulled apart to
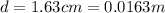`d=1.63 cm=0.0163 m`, so the capacitance becomes

`C=(1)(8.85\cdot 10^(-12)F/m)(0.210 m^2)/(0.0163 m)=1.1\cdot 10^(-10) F`