Question

These triangles are similar. Compare the first to the second and give the ratio of their areas. Write the ratio in simplest terms.

Answer options:9:25, 6:20, 3:5, 225:625

Answer 1

Option 1. 9: 25

Explanation:

It is given that the triangles are similar and their bases are 15 in. and 25 in. respectively.

We know in two similar triangles corresponding sides are in the same ratio.

Since base of the triangles are in the ratio of 15: 25 or 3: 5.

and the same ratio will be in their heights also that is 3: 5

Therefore area of the triangles will be

Area of 1 / Area of 2 = 1/2 (Base of 1)(height of 1)/1/2(Base of 2)(height of 2)

= (Base of 1)/(Bas of 2)× (height of 1)(height of 2)

=
`((3)/(5))((3)/(5)) = (9)/(25)`

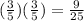
Therefore Option 1, 9: 25 is the correct option.

Answer 2

= 9 : 25

Explanation:

The triangles are similar.

The ratio of the corresponding sides is;

= 15 : 25

= 3 :5

This is equivalent to the linear scale factor

To get the ratio of their areas, we square the linear ratio;

= (3 : 5)²

= 9 : 25